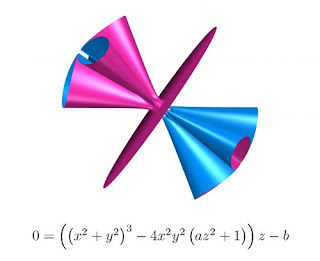Subo los apuntes de métodos numéricos. Fueron explicados en clase los días 26 y 27 de Noviembre.
sábado, 1 de diciembre de 2012
Aplicación de la derivada
En este vídeo se visualiza la aplicación de las matemáticas en una atracción de un parque. Donde nos explica el concepto de la derivada en el cálculo matemático y el álgebra analítica.
https://www.youtube.com/watch?feature=player_embedded&v=KSTxZ4fvVQQ#!
Tarea 18: Como medir la altura de un arbol
Es fácil medir la altura de un arbol usando solo una regla.
(Por semejanza de triángulos)
Medir la altura de un arbol, un edificio o cualquier otro objeto es relativamente sencillo si se dispone de una regla. El procedimiento es el siguiente:
1. Colocarse a una distancia conocida del objeto cuya altura H se quiere medir, en este caso el arbol. Llamamos D a esa distancia.
2. Extender el brazo mientras se sostiene una regla verticalmente a la altura de los ojos. Llamamos d a la distancia entre la mano y el ojo.
3. Cerrar uno de los ojos y con el restante determinar a cuantos centímetros de la regla corresponde la altura del arbol. A esa longitud medida en la regla la denominamos h.
Por semejanza de triángulos se obtiene que H/h = D/d. De esta relación se obtiene que la altura del arbol es:
Medir la altura de un arbol, un edificio o cualquier otro objeto es relativamente sencillo si se dispone de una regla. El procedimiento es el siguiente:
1. Colocarse a una distancia conocida del objeto cuya altura H se quiere medir, en este caso el arbol. Llamamos D a esa distancia.
2. Extender el brazo mientras se sostiene una regla verticalmente a la altura de los ojos. Llamamos d a la distancia entre la mano y el ojo.
3. Cerrar uno de los ojos y con el restante determinar a cuantos centímetros de la regla corresponde la altura del arbol. A esa longitud medida en la regla la denominamos h.
Por semejanza de triángulos se obtiene que H/h = D/d. De esta relación se obtiene que la altura del arbol es:
H = h.(D/d)
Como ejemplo supongamos que la distancia que nos separa del arbol es de 50 metros, que nuestro brazo extendido mide 60cm (0.6m) y que en la regla vimos que la altura relativa del arbol es de 20cm (0.2m), por lo tanto la altura real del arbol será
H = (0.2 x 50/0.6)m = 16.6m
H = (0.2 x 50/0.6)m = 16.6m
TAREA 18: La Helena de las curvas.
La curva cicloide ha sido considerada durante mucho tiempo una curva muy especial, tanto por sus fascinantes propiedades como por las disputas científicas que promovió principalmente a lo largo del siglo XVII. Tal es así que es conocida en la literatura como la Helena de la Geometría o la Helena de las curvas. Este sobrenombre le fue otorgado muy probablemente en honor a Helena de Troya, en relación bien con la belleza de ésta, bien con las disputas que ésta causó en vida. Según la mitología griega, Helena de Troya (esposa de Menelao, rey de Esparta) fue raptada por Paris (hijo menor de Príamo, rey de Troya), dando pie así a la famosa guerra de Troya, narrada en la Ilíada de Homero.
Una cicloide es el lugar geométrico (o curva) generado por un punto fijo de una circunferencia que rueda uniformemente y sin deslizamiento sobre una línea recta.

La braquistócrona es la cicloide. Dados dos puntos A y B, con A a una elevación mayor que B, existe solo una curva cicloide con la concavidad hacia arriba que pasa por A con pendiente infinita (dirección vertical y sentido de arriba hacia abajo), también pasa por B y no posee puntos máximos entre A y B. Esta particular cicloide invertida es una curva braquistócrona. la curva no depende de la masa del cuerpo o del valor de la constante gravitacional.
El problema puede ser resuelto utilizando los algoritmos del cálculo variacional.
Si al cuerpo se le da una velocidad inicial en A, o si se toma en cuenta el efecto de la fricción, la curva que minimiza el tiempo de tránsito será distinta de la descrita en los párrafos precedentes.


Visita al MUDIC:
Dispositivo experimental del siglo XVIII de Sigaud de Lafond para comprobar la minimalidad del tiempo de trayecto según una curva cicloide.
Fuentes:
- http://www.planetamatematico.com/index.php?option=com_content&task=view&id=348&Itemid=147
- http://es.wikipedia.org/wiki/Braquist%C3%B3crona
WebRep
Calificación general
Este sitio no tiene calificación
(no hay votos suficientes)
Tarea 18: Volumen de un toro
Un toro es una superficie de revolución generada
por una circunferencia que
gira alrededor de una recta exterior.
El toro genera un hueco en su interior, apropiando la forma semejante a un
neumático, el hueco central es
circular y tiene como radio R - r, lo que supone R > r.

Si R = r se obtiene una forma sin hueco central
parecida a una esfera desformada donde se juntarían los polos en su centro, y
no es topológicamente equivalente
a un toro usual.
Si R < r se obtiene una forma intermedia entre la anterior y una esfera (es decir que los polos se acercan pero no se tocan).
Si R < r se obtiene una forma intermedia entre la anterior y una esfera (es decir que los polos se acercan pero no se tocan).
Su volumen es V = 2·π2·r2·R
Su superficie es S = 4·π2·r ·R
Si se consideran la superficie y el
volumen como funciones S(r) y V(r) del radio, entonces se nota que la
superficie es la derivada del
volumen, y éste es una primitiva de
la superficie. Este hecho no es casualidad, pues se puede descomponer el
volumen en capas de espesor arbitrariamente pequeño dr, y los
volúmenes de estas capas se aproximan a S(r)·dr cuando dr tiende
hacia cero.
Sumando los volúmenes (infinitesimales) de todas estas capas (en cantidad infinita) cuando el radio r varía de cero a R da por definición la integral siguiente:
Sumando los volúmenes (infinitesimales) de todas estas capas (en cantidad infinita) cuando el radio r varía de cero a R da por definición la integral siguiente:
viernes, 30 de noviembre de 2012
LEY DE GAUSS
En física la ley de Gauss establece que el flujo de ciertos campos a través de una superficie cerrada es proporcional a la magnitud de las fuentes de dicho campo que hay en el interior de dicha superficie. Dichos campos son aquellos cuya intensidad decrece como la distancia a la fuente al cuadrado. La constante de proporcionalidad depende del sistema de unidades empleado.
Se aplica al campo electroestatico y al gravitatorio. Sus fuentes son la carga eléctrica y la masa, respectivamente. También puede aplicarse al campo magnetostático, aunque dicha aplicación no es de tanto interés como las dos anteriores.

http://commons.wikimedia.org/wiki/File:Electric_Flow_in_an_Ellipsoid.svg
VISUALIZACIÓN Y CÁLCULO DE VOLÚMENES DE SÓLIDOS DE REVOLUCIÓN CON WINPLOT
CALCULO Y VISUALIZACION DE VOLUMENES DE REVOLUCION CON WINPLOT®
En esta página te explican lo que son las volúmenes y te enseñan como hacerlas con el programa WINPLOT, esto es útil con el tema que estamos dando de áreas.
Fuente:
http://reyesestadistica.blogspot.com.es/2011/07/visualizacion-y-calculo-de-volumenes-de.html
http://reyesestadistica.blogspot.com.es/2011/07/visualizacion-y-calculo-de-volumenes-de_07.html
jueves, 29 de noviembre de 2012
TAREA 18: FIGURAS QUE REPRESENTAN UNA ECUACION
La Real Sociedad Matemáticas Española, a través de la exposición Imaginary, contribuye en el conocimiento y divulgación de las Matemáticas.
Consiste en un despliegue de exposiciones fijas interactivas , que muestran la relación entre la bellezas de las superficies , generadas a través de las matemáticas.
La muestra recoge 12 figuras en tres dimensiones creadas a partir del diálogo entre geometría y álgebra, dos de las principales ramas de las matemáticas.
Mediante un sistema de coordenadas (x, y, z) que permite orientarse en el espacio describiendo relaciones geométricas, se pueden representar figuras (geometría) con ecuaciones (álgebra), de una forma comprensible. De la convergencia entre álgebra y geometría surge una ecuación que puede dibujarse en el espacio. De hecho, muchas de estas formas geométricas bellas y armoniosas ya existen en la naturaleza de manera espontánea y por acumulación de ensayos. Gracias a las matemáticas, podemos analizarlas, desentrañar qué ecuaciones encierran y crear nuevas formas.
La idea es permitir que los usuarios experimenten con las matemáticas y creen bellas imágenes. De esta manera el visitante descubre por su cuenta las matemáticas subyacentes. Varios programas están disponibles en la exposición y en internet para ser descargados de forma gratuita. Los programas han sido desarrollados para IMAGINARY o adaptados especialmente.
Algunas de las formas de la exposición.
Enlace con información y para poder descargar los programas
desarrollados en la exposición:
Tarea 18: VOLUMEN DE UNA PIRAMIDE
Vídeo en el que podemos ver la demostración gráfica de que el volumen de una pirámide es un tercio del volumen de un prisma de la misma base y altura.
A lo largo del vídeo podemos ver que la suma de dos, de las tres cara de las caras de la pirámide, son la cara del prisma completo.
Los volúmenes de cada una de las pirámides son equivalentes entre sí, lo que demuestra que el volumen de una pirámide es la tercera parte del volumen de un prisma.
Fuente: youtube
http://www.youtube.com/watch?v=QNQKMyEBiuM
A lo largo del vídeo podemos ver que la suma de dos, de las tres cara de las caras de la pirámide, son la cara del prisma completo.
Los volúmenes de cada una de las pirámides son equivalentes entre sí, lo que demuestra que el volumen de una pirámide es la tercera parte del volumen de un prisma.
Fuente: youtube
http://www.youtube.com/watch?v=QNQKMyEBiuM
miércoles, 28 de noviembre de 2012
TAREA 18: VISUALIZACIÓN DE LOS VOLÚMENES DE REVOLUCIÓN
En este video del museo de la Universidad de Sonora podemos ver una representación de forma visual de los volúmenes de revolución.
Origami: arte + matemáticas + ciencia
Los origamis tradicionales los más «puros» son los que se construyen con hojas de papel cuadradas, en las que sólo se permiten pliegues (sin cortes ni pegamento). Esta limitación conlleva una mayor creatividad y elegancia.
Una investigación sobre el arte de los origamis descubrió ciertos axiomas matemáticos que gobiernan la creación de los milenarios origamis, algunos de los cuales se conocían desde la antigüedad, otros no. Mediante simulaciones por ordenador se descubrió que se podía crear prácticamente cualquier figura compleja reduciéndola de forma matemática a un esquema, siendo el ordenador el que exploraría esas fórmulas para indicar los pliegues en el papel, que luego el artista habría de realizar.
También hay también objetos cotidianos, poliedros y figuras geométricas, entre otras.
En la Sala Rekalde de Bilbao se encuentra estos "instantes plegados" de Mikel Varas. Hay que ver la figura en la sala para apreciar los pliegues, los ángulos, la superficie, la textura, el color, los detalles… de este bello cielo nublado.
Fuentes:
http://ztfnews.wordpress.com/2012/07/18/origami-en-acero/#more-8318
http://alefalletti.wordpress.com/2008/09/29/origami-arte-matematicas-ciencia-microsiervos-arte-y-diseno/
Una investigación sobre el arte de los origamis descubrió ciertos axiomas matemáticos que gobiernan la creación de los milenarios origamis, algunos de los cuales se conocían desde la antigüedad, otros no. Mediante simulaciones por ordenador se descubrió que se podía crear prácticamente cualquier figura compleja reduciéndola de forma matemática a un esquema, siendo el ordenador el que exploraría esas fórmulas para indicar los pliegues en el papel, que luego el artista habría de realizar.
También hay también objetos cotidianos, poliedros y figuras geométricas, entre otras.
En la Sala Rekalde de Bilbao se encuentra estos "instantes plegados" de Mikel Varas. Hay que ver la figura en la sala para apreciar los pliegues, los ángulos, la superficie, la textura, el color, los detalles… de este bello cielo nublado.
Fuentes:
http://ztfnews.wordpress.com/2012/07/18/origami-en-acero/#more-8318
http://alefalletti.wordpress.com/2008/09/29/origami-arte-matematicas-ciencia-microsiervos-arte-y-diseno/
martes, 27 de noviembre de 2012
Tarea 21 Área de una superficie
En este enlace hay un archivo PDF, con un superficie dibujada
https://docs.google.com/open?id=0B3Mcm7ktAEUWSWlib25YT3BKbzA
Queremos que calcules el área.
1º Por el método del punto medio con 2 intervalos
2º Por el método del punto medio con 4 intervalos
3º Por el método del trapecio con 2 intervalos
4º Por el método del trapecio con 4 intervalos
Plazo: hasta el 4 de Diciembre
Nota: Se entrega solamente por el formulario correspondiente
Valoración: 1 hora de trabajo.
https://docs.google.com/open?id=0B3Mcm7ktAEUWSWlib25YT3BKbzA
Queremos que calcules el área.
1º Por el método del punto medio con 2 intervalos
2º Por el método del punto medio con 4 intervalos
3º Por el método del trapecio con 2 intervalos
4º Por el método del trapecio con 4 intervalos
Plazo: hasta el 4 de Diciembre
Nota: Se entrega solamente por el formulario correspondiente
Valoración: 1 hora de trabajo.
Máquina de Galton
El pasado sábado 24 de noviembre en el museo MUDIC, nos encontramos con una máquina en la que podias ver una demostración mecánica de probabilidad. Esta maquina recibe el nombre de máquina de Galton.
Sir Francis Galton (1822-1917) nació en Birmingham. sus trabajos más importantes conectaron con sus dos grandes aficiones: el estudio de la herencia y la expresión matemática de los fenómenos vinculados a ella.
Galton diseñó un curioso aparato en el que una colección de bolitas descienden de manera aleatoria, cada vez que una bola llega a una bifurcación se desvía hacia la derecha o hacia la izquierda con la misma probabilidad. Las bolitas se van acumulando en la parte inferior y van dibujando una silueta que, si el numero de bolitas y el de cajas es grande, cada vez se parece más a una curva, que recibe el nombre de curva normal.
A continuación, podemos ver como funciona la máquina de Galton:
Información y Fotografía; Museo Mudic
Vídeo: www.youtube.com
Máquina de Galton.
1)Breve descripción del Modelo- Está constituída por una tabla vertical con numerosas filas de clavos intercalados sucesivamente. Caen por los espacios entre clavos 800 bolillas de acero. Al pasar de fila en fila la probabilidad de caer a derecha o izquierda de un clavo es de un medio. Componiendo consecutivamente todas estas probabilidades en la caída de una bolilla, para todas las bolillas se cumple una distribución normal Gaussiana.
2)Conceptos Matemáticos en juego- evento probabilidad distribución de probabilidad distribución gaussiana
3)Guía de Uso Específica del Modelo- Qué y Cómo hay que mover o realizar. Se ordenan las bolillas para la experiencia SÓLO MOVIENDO LATERALMENTE AL APARATO. Cuando están en posición se lo coloca vertical para que caigan las bolillas. Qué hay que observar. La forma del apilamiento de las bolillas en las troneras. Qué precauciónes se deben tener. No esforzar hacia adelante al aparato.Para ordenar las bolillas insistir con giros laterales.
4)Breves referencias teórico-técnicas-
Máquina de probabilidades de Galton , programa de simulación.

TAREA 18. MUSEO MATEMATICO
En la provincia de Cataluña, existe un museo dedicado a las matemáticas, en el podemos encontrar varios experimentos y exposiciones.
http://www.mmaca.cat/
Uno de los experimentos el cual me ha parecido interesantes es el de las parábolas de agua, en el cual, de la misma manera que los proyectiles o cualquier objeto sometido a la fuerza de la gravedad y a la vez lanzado con una fuerza inicial con una componente horizontal, el agua al caer dibuja una parábola.
Las parábolas dibujadas por los agujeros del lado derecho tienen diferente amplitud porque son dentro de un mismo depósito y la presión depende de la altura de la columna de agua. En cambio, las parábolas de los agujeros de la izquierda son todas iguales ya que los agujeros están dentro de depósitos independientes todos a la misma profundidad.
http://www.mmaca.cat/
Uno de los experimentos el cual me ha parecido interesantes es el de las parábolas de agua, en el cual, de la misma manera que los proyectiles o cualquier objeto sometido a la fuerza de la gravedad y a la vez lanzado con una fuerza inicial con una componente horizontal, el agua al caer dibuja una parábola.
Las parábolas dibujadas por los agujeros del lado derecho tienen diferente amplitud porque son dentro de un mismo depósito y la presión depende de la altura de la columna de agua. En cambio, las parábolas de los agujeros de la izquierda son todas iguales ya que los agujeros están dentro de depósitos independientes todos a la misma profundidad.
lunes, 26 de noviembre de 2012
EL BILLAR ELIPTICO
Como vemos en la imagen el billar tiene forma de elipse. En el museo nos explicaron el funcionamiento que tiene.Si situas dos bolas una en cada foco del elipse siempre que le des a una bola de un foco al rebotar en cualquier punto del borde siempre le daras a la otra bola que esta situada en el otro foco.
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución. Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.

Elipse en un nido:
Como vemos en la imagen el billar tiene forma de elipse. En el museo nos explicaron el funcionamiento que tiene.Si situas dos bolas una en cada foco del elipse siempre que le des a una bola de un foco al rebotar en cualquier punto del borde siempre le daras a la otra bola que esta situada en el otro foco.
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución. Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.

Elipse en un nido:
Tarea Nº 19 Volumen de un toro
Queremos calcular el volumen de un toro matemático. Para ello lo haremos como un volumen de revolución sobre el eje 0X, Los extremos serán -1 y 1, y las funciones:
Este ejercicio hay que entregar en papel, los cálculos deberías de hacerlo utilizando el Wolfran Alpha.
Por tanto entregar en papel, y rellenar el formulario correspondiente
Valoración: 1 hora
Plazo: hasta el 4 de diciembre
domingo, 25 de noviembre de 2012
Experimentos de Probabilidad
http://es.scribd.com/doc/84684529/Matematicas-Experimentales-UNESCO
He econtrado experimentos matemáticos que se pueden realizar en casa, el que más me ha llamado la atención es el de la página 95 que habla de probabilidad.
Aplicaciones de las matemáticas
He econtrado experimentos matemáticos que se pueden realizar en casa, el que más me ha llamado la atención es el de la página 95 que habla de probabilidad.
Aplicaciones de las matemáticas
Hoy en día la probabilidad y la estadística se utilizan en la gestión de sistemas complejos: control decohetes, colas de espera, márgenes de error, etc.Pero también en juegos con dinero, en economía, seguros, cálculo de jubilaciones y planes de jubilación,tests de calidad, estudios de opinión, etc.El cálculo estadístico permite extrapolar información para una población completa a partir de una muestra representativa. Los sondeos bien llevados deben también informar sobre los límites de lastécnicas utilizadas.
La máquina de Galton
La máquina de Galton nos muestra la curva de distribución normal (campana de Gauss).
Idealmente la probabilidad de que una esfera caiga a la izquierda o derecha es la misma, por lo cual es poco probable que los rebotes de las esferas sean todos a la izquierda o a la derecha. Por ello, en la mayoría de los casos la concentración de las esferas es en la parte central.
La campana de Gauss es un modelo de distribución de probabilidad descrito por el matemático y físico alemán Carl Friederich Gauss (1777-1855).
Esta curva, también conocida como distribución normal es una función de probabilidad continua y simétrica, cuyo máximo es la media y tiene dos puntos de inflexión situados en ambos laados. Un punto de inflexión es el que separa la parte cóncava de la convexa de la campana.
Esta gráfica representa el acomportamiento de los valores de una población o universo de eventos, cuyas variacionses sólo están influenciadas por fenómenos aleatorios.
Muestra es un valor representativo del conjunto total llamado universo o población.
Frecuencia es el número de veces que cada valor se repite.
Moda es el valor que más se repite.
Promedio o media (m) es el cociente de la suma de todos los valores entre la cantidad de valores.
Mediana es el valor que ocupa la posición central, cuando los valores se ordenan de mayor a menor.
Desviación estandár (s) es una medida de qué tanto se dispersan los valores, alejándose mucho o poco de la media.
Los parámetros necesarios para dibujar el gráfico de la distribución normal son m y s, con los cuales sabemos dónde situar la campana de Gauss (punto correspondiente a m) y cuál es su ancho (determinado por s) .

En esta exhibición, se tienen 2,166 balines y 43 casillas. Cada balín que cae en alguna de las casillas, es un evento.
La moda es 21, porque corresponde al número de casilla que registra una mayor frecuencia; también es la mediana, pues es la que ocupa la posición central.
El promedio se obtiene de dividir la suma acumulada del producto del número de casilla por la cantidad de balines que contiene, entre el número total de eventos.

Área bajo la curva
Desviación
Fracción total de área incluída
0.675
50.00 %
1.0
68.28 %
2.0
95.46 %
3.0
99.72 %
4.0
99.99 %
100 %
La variable de la cual se pretende estudiar su comportamiento, es el número de casilla (c).
NOTA: Los valores cambian cada vez que se realiza el experimento.
Los valores aquí mostrados corresponden a un ejemplo del experimento real.

Fuentes:
Idealmente la probabilidad de que una esfera caiga a la izquierda o derecha es la misma, por lo cual es poco probable que los rebotes de las esferas sean todos a la izquierda o a la derecha. Por ello, en la mayoría de los casos la concentración de las esferas es en la parte central.
La campana de Gauss es un modelo de distribución de probabilidad descrito por el matemático y físico alemán Carl Friederich Gauss (1777-1855).
Esta curva, también conocida como distribución normal es una función de probabilidad continua y simétrica, cuyo máximo es la media y tiene dos puntos de inflexión situados en ambos laados. Un punto de inflexión es el que separa la parte cóncava de la convexa de la campana.
Esta gráfica representa el acomportamiento de los valores de una población o universo de eventos, cuyas variacionses sólo están influenciadas por fenómenos aleatorios.
Muestra es un valor representativo del conjunto total llamado universo o población.
Frecuencia es el número de veces que cada valor se repite.
Moda es el valor que más se repite.
Promedio o media (m) es el cociente de la suma de todos los valores entre la cantidad de valores.
Mediana es el valor que ocupa la posición central, cuando los valores se ordenan de mayor a menor.
Desviación estandár (s) es una medida de qué tanto se dispersan los valores, alejándose mucho o poco de la media.
Los parámetros necesarios para dibujar el gráfico de la distribución normal son m y s, con los cuales sabemos dónde situar la campana de Gauss (punto correspondiente a m) y cuál es su ancho (determinado por s) .

En esta exhibición, se tienen 2,166 balines y 43 casillas. Cada balín que cae en alguna de las casillas, es un evento.
La moda es 21, porque corresponde al número de casilla que registra una mayor frecuencia; también es la mediana, pues es la que ocupa la posición central.
El promedio se obtiene de dividir la suma acumulada del producto del número de casilla por la cantidad de balines que contiene, entre el número total de eventos.

Área bajo la curva
Desviación
Fracción total de área incluída
0.675
50.00 %
1.0
68.28 %
2.0
95.46 %
3.0
99.72 %
4.0
99.99 %
100 %
La variable de la cual se pretende estudiar su comportamiento, es el número de casilla (c).
NOTA: Los valores cambian cada vez que se realiza el experimento.
Los valores aquí mostrados corresponden a un ejemplo del experimento real.

Fuentes:
Mudic, youtube, http://www.cedicyt.ipn.mx/museo/gauss.html
Suscribirse a:
Entradas (Atom)